Tot això esta molt bé pero com es pot trobar el nombre d'or "phi"?
Hi ha moltes maneres pero explicaré les més sencilles:
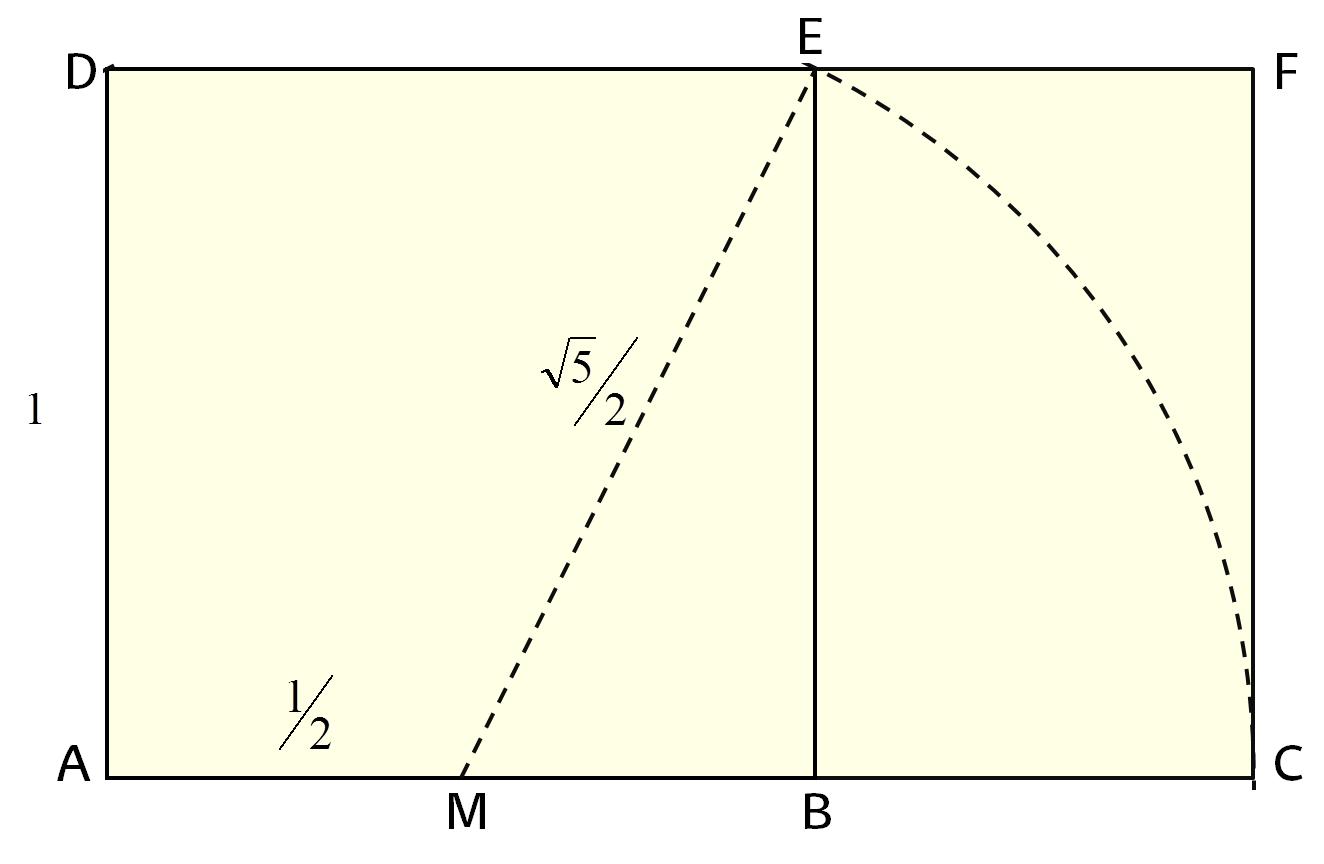
La primera consisteix en agafar l'aresta d'un quadrat i dividir-la entre 2. Aquest punt sera el centre d'una circumferència que tendra com radi la distància al vèrtex contrari. Si allarguem la aresta on esta el centre fins que es talli amb la circumferència i agafem la suma de l'aresta mes la seva prolongació tindrem la base d'un rectangle. Si dividim aquesta amplada entre l'altura inicial del quadrat la proporció sempre sera de 1,618... el nombre phi. El rectangle que queda s'anomena "Rectangle d'or".
Si agafes dos nombres (minimament grans) d'aquesta successió com el 1597 i el 2584 i els divideixes entre ells tindras com resultat el nombre d'or. Com més grans siguin els dos nombres, el resultat sera més exacte a phi.
2584÷1597=1,6180338...
Per últim, una tercera manera de trobar aquest nombre és fer l'arrel de 1 més (dins la mateixa arrel) una arrel de 1 que tambè esta sumada amb una arrel de 1 i així fins a l'infinit. Dit així sembla dificil però amb l'exemple s'enten molt millor. Com més llarga sigui l'operació, més exacte és.
Hi ha moltes més maneres de trobar el nombre d'or però aquestes són les més sencilles que pots comprobar tu mateix agafant una calculadora o dibuixant el primer exemple i comprovant la proporció.
Per últim, una tercera manera de trobar aquest nombre és fer l'arrel de 1 més (dins la mateixa arrel) una arrel de 1 que tambè esta sumada amb una arrel de 1 i així fins a l'infinit. Dit així sembla dificil però amb l'exemple s'enten molt millor. Com més llarga sigui l'operació, més exacte és.
Hi ha moltes més maneres de trobar el nombre d'or però aquestes són les més sencilles que pots comprobar tu mateix agafant una calculadora o dibuixant el primer exemple i comprovant la proporció.
